Решение задач на динамику

Понимание первого закона Ньютона проверяется, как правило, двумя способами:

1. Описывается ситуация и необходимо выбрать, в каком случае ту или иную систему отсчета можно считать инерциальной. В этом случае инерциальной можно считать только ту систему отсчета, которая движется относительно Земли (принимаемой за ИСО) прямолинейно и равномерно.
2. Описывается ситуация, в которой тело движется прямолинейно и равномерно. При этом рассматриваются действующие на него силы. Ответы к заданиям проверяют понимание того факта, что в инерциальных системах отсчета тело покоится или движется равномерно и прямолинейно в том случае, если действие всех сил на него скомпенсировано.

Пример. Самолёт летит по прямой на высоте 9000 м. Систему отсчета, связанную с Землей, считать инерциальной. В этом случае:

1. на него не действует сила тяжести
2. сумма всех сил, действующих на самолет, равна нулю
3. на самолет не действуют никакие силы
4. сила тяжести равна силе Архимеда, действующей на самолет.

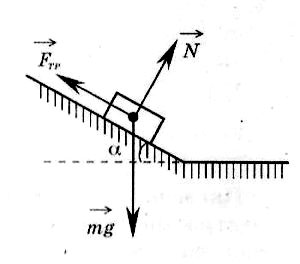Пример. Брусок лежит на шероховатой наклонной опоре (см. рисунок). На него действуют 3 силы: сила тяжести mg, сила упругости опоры N и сила трения F_тр. Если брусок покоится, то модуль равнодействующей силы трения равен
1) mg 2) F_тр + N 3) NCosα 4) F_тр Sinα
Строго говоря на брусок действуют две силы - сила тяжести и сила реакции опоры, но в школьной методике принято делить общую силу реакции на силу трения и силу нормальной реакции (или силу упругости) опоры. Если тело покоится относительно выбранной ИСО или движется равномерно и прямолинейно, то векторная сумма всех сил будет равна нулю, а векторная сумма любых двух сил будет равна третьей.

Одна из главных идей динамики Галилея-Ньютона: сила определяет изменение скорости, т.е. ускорение, а не скорость. Поэтому при проверке второго закона Ньютона в заданиях достаточно часто предлагается ответить на вопрос о сонаправленности векторов равнодействующей силы и ускорения. При этом возможны различные формы представления информации в заданиях.

Пример. Какие из величин (скорость, сила, ускорение, перемещение) при механическом движении всегда совпадают при движении?

1) сила и перемещение; 2) сила и скорость; 3) сила и ускорение; 4) ускорение и скорость.

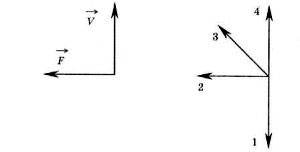
Пример. На рисунке представлены вектор скорости и вектор равнодействующей всех сил, действующих на тело. Какой из четырех векторов на правом рисунке указывает направление вектора ускорения этого тела в инерциальных системах отсчета? 1) 1 2) 2 3) 3 4) 4

Много ошибок бывает в заданиях на понимание того, что ускорение вызывается равнодействующей всех сил.

Пример. Груз, привязанный к нити, двигался по окружности с центростремительным ускорением 4 м/с². С каким ускорением будет двигаться груз сразу после обрыва нити?
1) 4 м/с²2) 14 м/с²3) 10 м/с²4) √(10²+4²) м/с²
После обрыва нити на груз действует только сила тяжести, а следовательно, ускорение его равно ускорению свободного падения (10 м/с²— ответ 3).

При повторении закона всемирного тяготения следует обратить внимание на расчет гравитационной силы, действующей на тело, которое расположено на некотором расстоянии от поверхности Земли (нужно помнить, что расстояние отсчитывается от центра Земли, а не от ее поверхности).

Пример. У поверхности Земли на космонавта действует гравитационная сила 720 Н. Какая гравитационная сила действует со стороны Земли на того же космонавта в космическом корабле, который с помощью реактивных двигателей удерживается неподвижно относительно Земли на расстоянии двух ее радиусов от земной поверхности?
1) 360Н 2) 240Н 3) 180Н 4) 80Н
Здесь сила 720 Н действует на расстоянии R, а затем тело перенесли на расстояние 3R от центра земли, поэтому сила уменьшилась в 9 раз.

Для выполнения заданий на проверку понимания силы трения скольжения нужно учитывать следующие моменты:
Сила трения скольжения не зависит от площади опоры, т.е. если в задании брусок равномерно движется по одной и той же поверхности и его поворачивают при этом разными гранями, то сила трения скольжения не меняется.
Сила трения скольжения связана соотношением F = µN с нормальной силой упругости опоры. Поэтому нельзя автоматически использовать формулу F = µmg, а нужно сначала определить силу реакции опоры, а затем уже вычислять силу трения. Например, в случае, приведенном на первом рисунке, сила трения будет уменьшаться за счет действия силы тяги и равна µ(mg-Fsinα), а во втором случае, наоборот, будет увеличиваться и равна µ(mg+Fsinα).
В приведенном ниже задании ускорение должно быть таким, чтобы обеспечивать силу реакции опоры, при которой сила трения будет (при минимальном ускорении) равной силе тяжести.

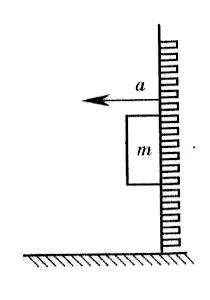Пример. К подвижной вертикальной стенке приложили груз массой 10 кг. Коэффициент трения между грузом и стенкой равен 0,4. С каким минимальным ускорением надо передвигать стенку влево, чтобы груз не соскользнул вниз?
ma=N; Fтр=µN; mg=Fтр. Следовательно, ускорение равно 25 м/с².


« Все материалы »