Из двух математических маятников один совершил 10 колебаний, а другой за то же время 6 колебаний. Найти длину каждого маятника, если сумма их длин равна 42,5 см.
В результате получится система уравнений с двумя переменными. Решение прилагается.
Период математического маятника равен
Т = 2π√(l/g)
T₁ = 2π√(l₁/g)
T₂ = 2π√(l₂/g)
По условию задачи:
10T₁ = 6T₂
или
10√l₁ = 6√l₂
100l₁ = 36l₂
l₁ = 0.36l₂
Сумма длин маятников:
l₁ + l₂ = 42,5
или
0.36l₂ + l₂ = 42,5
1,36 l₂ = 42,5
l₂ = 31,25(см)
l₁ = 0.36l₂ = 0.36·31,25 = 11,25(см)
Ответ: длины маятников: l₁ = 11,25см, l₂ = 31,25см
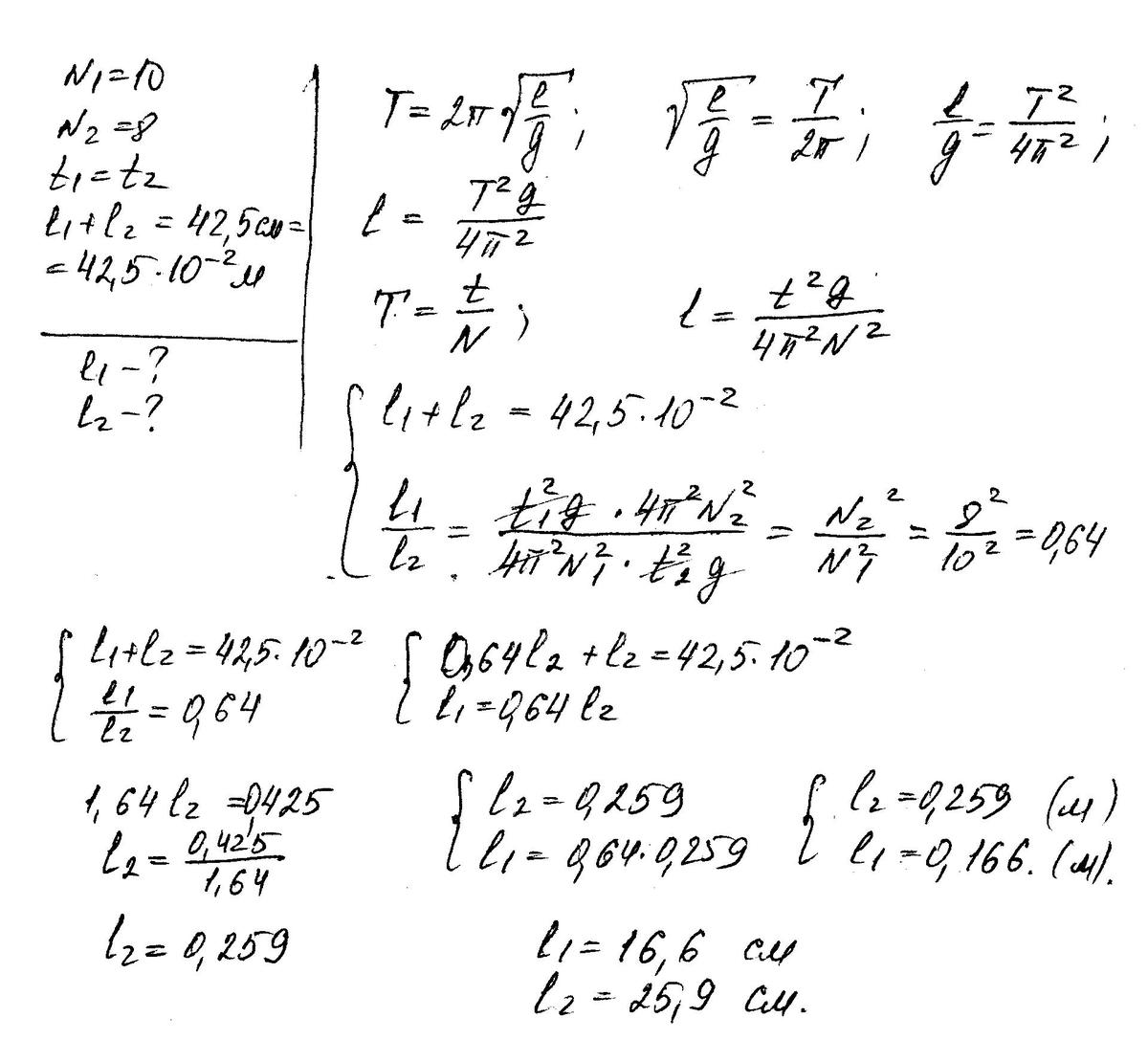
ПОХОЖИЕ ЗАДАНИЯ:
