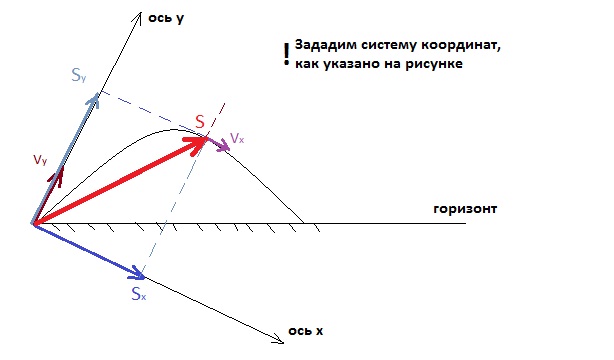
1. Введем прямоуголную систему координат следующим образом, полож. Нарпавление оси Оу совпадает с направлением начальной скорости тела, а полож. Направление оси Ох совпадает с направлением скорости тела через 5 с, то есть перпендикулярно (по усл. )

2. В векторном виде: S(суммарное)=S(по оси Ох)+S(по оси Оу).

Т. К. Угол между векторами 90, то S(суммарное) найдем по теореме Пифагора, зная перемещение вдоль оси Ох, и перемещение вдоль оси Оу.

3. Пусть v0 - начальная скорость, v - скорость тела через время t=5с, y - перемещение тела вдоль оси Оу, х - перемещение тела вдоль оси Ох, угол а - угол между вектором v0 и горизонтом, (а также угол между вектором g и осью Ох), тогда:

Oy:  0=v0-g*sin a*t, где t = 5 c, то есть v0=g*sin a*t

Ox:  v=0+g* cos a*t, то есть v=g*cos a*t

y=v0*t - ( g*sina*t^2/2 ); так как v0=g*sin a*t, то:

y = ( g*sina*t^2 - (g*sina*t^2)/2 = (g*sina*t^2)/2 )

x=( (g*cosa*t^2)/2 )

4. s=√( y^2+x^2 )

s=( (g*t^2)/2 )√c( cos^2a+sin^2a ), согласно основному тригонометрическому тождеству выражение под корнем равно 1, следовательно корень равен 1, а значит:

s=( (g*t^2)/2 )

s=10*5*5/2=125(м)

Ответ: 125 м