Механические колебания и волны
В этой теме следует обратить внимание на умение записывать уравнение гармонических колебаний по заданным амплитуде и периоду колебаний и, с другой стороны - определять параметры (амплитуду, частоту, период, начальную фазу) по уравнению гармонических колебаний. Кроме того, нужно уметь находить параметры колебаний по заданному графику зависимости координаты от времени или, например, по графику зависимости амплитуды установившихся колебаний маятника от частоты вынуждающей силы (резонансная кривая). Те же умения проверяются в вариантах ЕГЭ и для волн.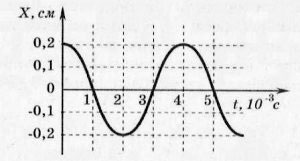
В этом случае амплитуда 0,2 см, период 4 миллисекунды, частота 250 Гц.
Для математического и пружинного маятников следует четко представлять, oт каких величин зависит период их колебаний, а от каких нет.
Например, в задании «Как изменится период колебаний математического маятника, если длину его нити уменьшить в 4 раза, а массу увеличить в 2 раза?» ответ будет «уменьшится в 2 раза», так как от массы период колебаний математического маятника не зависит.
Крайне сложными оказываются задания, в которых изменяется ускорение свободного падения (маятник поднимают на гору, опускают в шахту и т.п.) и спрашивают, как изменится ход маятниковых часов). При этом следует помнить, что, если период колебаний увеличится, то ход часов замедлится, и они будут отставать.
Пример. Если на некоторой планете период колебаний секундного земного математического маятника окажется равным 2 с, то ускорение свободного падения на этой планете примерно равно
1) 2,5 м/с 2 2) 4,9 м/с 2 3) 19,6 м/с 2 4) 39,2 м/с 2.
