Кинематика: задачи на движение

В заданиях на определение относительной скорости нужно обращать внимание на направления движения тел. Например, в условии задачи "Два автомобиля движутся по прямой дороге: один со скоростью 50 км/ч, а другой — со скоростью 70 км/ч" не указано направление движения, поэтому автомобили могут как сближаться, так и удаляться.

Наибольшие затруднения вызывают задания на определение относительной скорости в случае движения тел под углом 90⁰ друг к другу.

Пример. Лодка должна попасть на противоположный берег реки по кратчайшему пути в системе отсчета, связанной с берегом. Скорость течения реки и, а скорость лодки относительно воды υ. Модуль скорости лодки относительно берега должен быть ранен 1) υ+и 2) υ—и 3) √ υ² +и² 4) √ υ² -и².

Для выполнения таких заданий следует повторить правила сложения векторов и помнить геометрические соотношения для прямоугольного треугольника. Кроме этого, для более ясно понимания того что происходит в задаче желательно поставить себя на место того тела относительно кторого решается задача.

В заданиях по кинематике используются разные способы задания характера движения тел, поэтому нужно уметь читать как уравнения, отражающие зависимость скорости или пути от времени в символическом виде, так и соответствующие графики.

Пример. Зависимость пути от времени для прямолинейно движущегося тела имеет вид: s(t) = 2t+3t², где все величины выражены в СИ. Ускорение тела равно 1) 1 м/c² 2) 2 м/c² 3) 3 м/c² 4) 6 м/c² В этом задании необходимо понимать, что об ускорении говорит коэффициент при t² и он равен половине ускорения.

При выполнении заданий с использованием графиков следует сначала определить вид движения (равномерное или равноускоренное), а уже затем делать вычисления, используя соответствующие формулы.

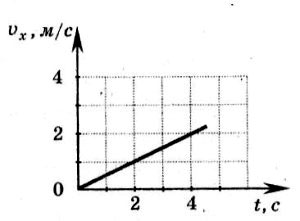Пример. Тело движется по оси ОХ. Проекция его скорости и_x(t)меняется по закону, приведенному на графике. Путь, пройденный телом за 2 с, равен 1) 1 м 2) 2 м 3) 4 м 4) 8 м

Поскольку движение тела равноускоренное, то по графику определяем ускорение 0,5 м/с², а затем вычисляем путь — 1 м. Но гораздо проще воспользоваться графическим методом, определив площадь треугольника, которая и будет равна искомому пути.

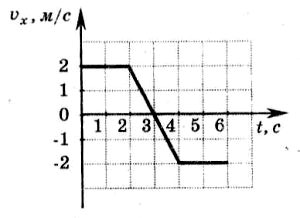Пример. Па графике изображена зависимость проекции скорости тела, движущегося вдоль оси ОХ, от времени. Какой путь прошло тело к моменту времени t=6c? 1)0 м 2) 6 м 3) 8 м 4) 10 м.
Эта задача решается графически. Но здесь необходимо обратить внимание на то, что искомой величиной является путь (величина всегда положительная), который равен 10 м, а не перемещение (чтобы не попасться в ловушку первого ответа — 0).

При выполнении заданий на движение по окружности с постоянной скоростью нужно помнить формулы для центростремительного ускорения (через линейную и угловую скорости), для периода и частоты обращения. В этом случае задания типа, приведенного ниже, не будут вызывать сложностей.

Пример. Две материальные точки движутся по окружностям радиусами R₁ и R₂=2R₁ с одинаковыми скоростями. Определите, как связаны их периоды обращения (центростремительные ускорения)?
Отношение периодов обращения равно отношению радиусов, поэтому T₁=T₂/2, а отношение ускорений равно обратному отношению радиусов: а₁=2а₂.

« Все материалы »