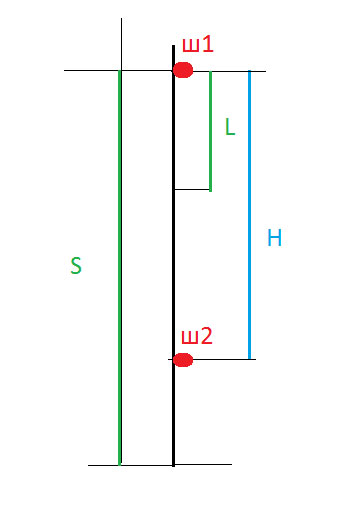
Когда шарик, падающий с вершины башни, полетел L метров, другой шарик начал падать из точки, расположенной на H метров ниже вершины. Чему равна высота башни, если шарики упали одновременно? РЕШЕНИЕ, ПОЯСНЕНИЕ, ОТВЕТ
ДАНО
L
H
-
S -
РЕШЕНИЕ
Обозначим S- высота башни
Сразу понятно, что L не равно H.(см на рисунке)
ШАРИК 1
начальная скорость V1o=0
в конце отрезка L имеет скорость V (найдем, нужда для решения)
L=(V^2-V1o^2)/2g=V^2/2g
V=√(2gL) (1)
за остальное время t - шарик 1 пролетел расстояние S-L (с начальной скоростью V)
S- L = Vt +gt^2/2 (2)
ШАРИК 2
начальная скорость V2o=0
S- H высота, с которой началось падение
падение длилось тоже время t
S-H = V2ot +gt^2/2 = gt^2/2 (3)
S-H = gt^2/2
t^2 =2(S-H)/g
t =√(2(S-H)/g ) (4)
подставим (1)(3)и(4) в (2)
S- L = Vt +gt^2/2 = √(2gL) *√(2(S-H)/g ) + (S-H)
S- L- (S-H) = √(2gL) *√(2(S-H)/g)
H-L =√(4L(S-H))
(H-L)^2 =4L(S-H)
S-H=(H-L)^2 /(4L)
S= (H-L)^2 /(4L) + H
Ответ высота башни (H-L)^2 /(4L) + H
ПОХОЖИЕ ЗАДАНИЯ:
